NLP Course - Neural Language Models Notebook

Table of Contents

Introduction to Neural Language Models

A neural language model (NLM) is a machine learning model used in natural language processing (NLP) to predict the probability of a sequence of words or the next word in a sequence. Unlike traditional statistical models like n-grams, NLMs use neural networks to learn complex patterns in text, capturing both semantic (meaning) and syntactic (grammar) relationships.

Key Concepts

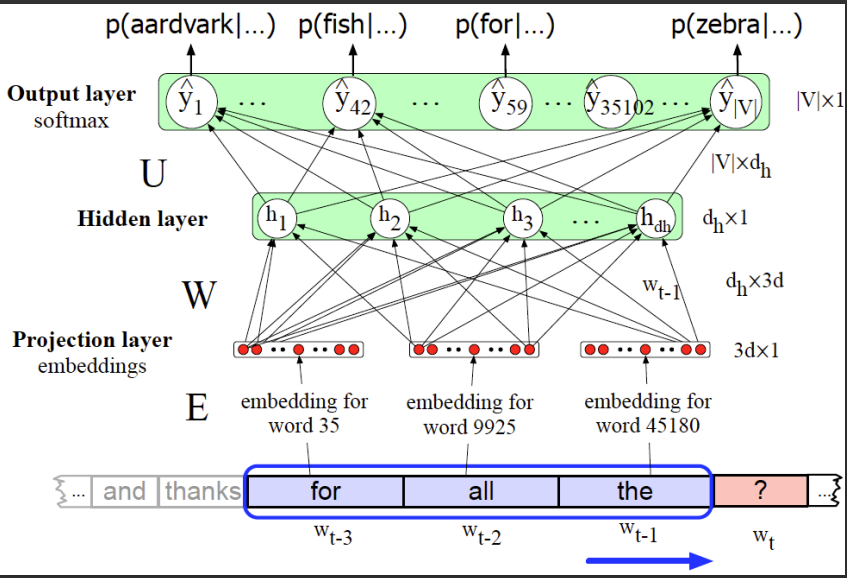
How Neural Language Models Work

Neural language models take a sequence of words, process them through a neural network, and output probabilities for the next word. For someone new to this, think of it like a smart system that learns from examples to guess the next word in a sentence. Here’s how it works step-by-step:

Step-by-Step Process

  1. Input Text: Start with a sequence of words, like "The cat is".
  2. Word Embeddings: Convert each word into a numerical vector that captures its meaning (e.g., "cat" might become [0.1, -0.3, 0.5]).
  3. Neural Network Layers: Pass these vectors through layers (like fully connected layers) to learn patterns in the sequence.
  4. Output Layer: Use a softmax function to produce a probability for each possible next word in the vocabulary.
  5. Training: Adjust the model’s parameters (weights) to make better predictions by minimizing errors using a loss function, like cross-entropy.

The model learns by seeing many sentences and tweaking its internal settings to improve its guesses.

Word Embeddings

Neural networks can’t process words directly because they’re text, not numbers. Word embeddings solve this by turning words into dense vectors (lists of numbers) that represent their meaning in a numerical space. Words with similar meanings (like "king" and "queen") have similar vectors.

How Embeddings Work

Example Code

import numpy as np # Simulated word embeddings (pre-trained) vocab = {"the": 0, "cat": 1, "is": 2} embedding_matrix = np.array([ [0.2, -0.1, 0.4], # "the" [0.1, -0.3, 0.5], # "cat" [0.3, 0.2, -0.2] # "is" ]) word = "cat" embedding = embedding_matrix[vocab[word]] print(f"Embedding for '{word}':", embedding)

Softmax Function

The softmax function is used in the output layer of a neural language model to turn raw scores (called logits) into probabilities for each word in the vocabulary. These probabilities sum to 1 and show how likely each word is to be the next word.

Intuitive Explanation

Imagine you have scores for possible next words: 2.5 for "jumps", 1.0 for "sleeps", and -0.5 for "runs". The softmax function makes these scores positive and scales them so they add up to 1. For example, it might give 0.7 for "jumps", 0.2 for "sleeps", and 0.1 for "runs". It boosts higher scores while still giving small probabilities to less likely words.

Mathematical Formulation

For a vector of logits z = [z₁, z₂, ..., zₙ], the softmax function computes the probability for the i-th word as:

P(y=i) = e^{zᵢ} / ∑_{j=1}^n e^{zⱼ}

Here, e^{zᵢ} is the exponential of the i-th logit, making all values positive. The denominator sums the exponentials of all logits to normalize the probabilities.

Key Points

Example Code

import numpy as np def softmax(logits): exp_logits = np.exp(logits) return exp_logits / np.sum(exp_logits) logits = np.array([2.5, 1.0, -0.5]) # Scores for "jumps", "sleeps", "runs" probs = softmax(logits) print("Logits:", logits) print("Probabilities:", probs) print("Sum of probabilities:", np.sum(probs))

Activation Functions

Activation functions add non-linearity to neural networks, allowing them to learn complex patterns. Without them, a neural network would just be a series of linear transformations, which can’t model things like the relationships between words in a sentence. They decide whether a neuron should "fire" or pass information forward.

Common Activation Functions

Example Code

import numpy as np def sigmoid(x): return 1 / (1 + np.exp(-x)) def relu(x): return np.maximum(0, x) def tanh(x): return np.tanh(x) x = np.array([-2, -1, 0, 1, 2]) print("Input:", x) print("Sigmoid:", sigmoid(x)) print("ReLU:", relu(x)) print("Tanh:", tanh(x))

Why Tanh is Widely Used

The hyperbolic tangent (tanh) activation function is commonly used in neural language models, especially in early models, for several reasons:

While modern models often use ReLU or its variants for faster training, tanh remains popular in recurrent neural networks (RNNs) and early NLP models due to its balanced properties.

Fixed Window Problem

Basic neural language models often use a fixed-size context window (e.g., the previous n words) to predict the next word. This approach has limitations:

These limitations make fixed-window models less effective for long sequences. Recurrent Neural Networks (RNNs), which maintain a hidden state to remember past information, address this issue by processing sequences of arbitrary length. We’ll cover RNNs in the next notebook.

Practical Example

Let’s implement a simple neural language model using a feedforward neural network with word embeddings, a hidden layer with tanh activation, and a softmax output layer. The model predicts the next word given a context of two words (bigram). We define a small vocabulary and simulated data, initialize embeddings and weights, and perform a forward pass to compute probabilities and loss. This is a simplified example; real models would include a full training loop and optimization.

Created by wikm.ir with ❤️