NLP Course - Self-Attention and Positional Encoding

Introduction to Self-Attention

In the previous notebook, we learned about the Attention mechanism, which allows a model to focus on relevant parts of an input sequence when generating an output, like focusing on "cat" when translating "The cat is on the mat" to "chat" in French. Self-Attention, introduced in the Transformer model by Vaswani et al. (2017), is a special type of Attention where the model attends to all words in the same sequence to understand their relationships.

Imagine reading a sentence: "The cat, which is fluffy, sleeps." To understand "fluffy," you need to connect it to "cat," not "sleeps." Self-Attention enables each word in the sentence to "look" at every other word, computing how much each word (e.g., "cat") influences the representation of another word (e.g., "fluffy"). This is done using queries, keys, and values, as introduced in the previous notebook.

In Self-Attention, for each word in the input sequence, the model:

• Creates a query vector qᵢ to represent what the word is "asking" about.
• Creates a key vector kᵢ to represent what the word "offers" in terms of relevance.
• Creates a value vector vᵢ to represent the word’s content.

These vectors are used to compute attention weights, which determine how much each word contributes to the representation of every other word, forming a new, context-aware representation for each word.

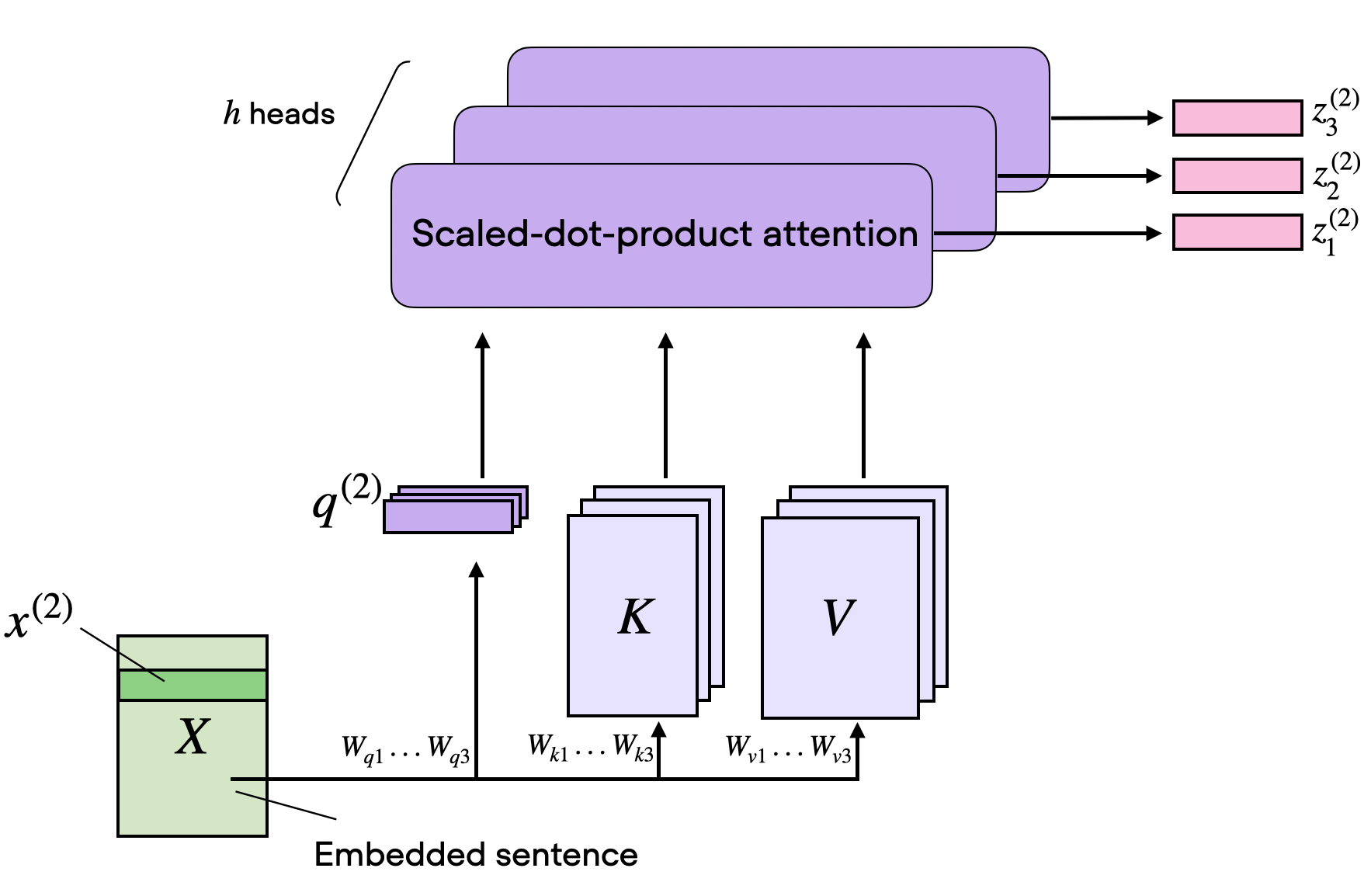
Why Use Self-Attention?

Self-Attention is a cornerstone of modern NLP models like Transformers because it addresses limitations of previous approaches, such as RNNs and standard Attention in Seq2Seq models:

• Parallel Processing: Unlike RNNs, which process words sequentially, Self-Attention computes relationships between all words simultaneously, making it faster on GPUs.
• Long-Range Dependencies: Self-Attention directly connects every word to every other word, capturing relationships (e.g., between "cat" and "fluffy") regardless of their distance, unlike RNNs, which struggle with long sequences due to vanishing gradients.
• Contextual Understanding: By allowing each word to attend to all others, Self-Attention creates rich, context-aware representations, improving tasks like translation, summarization, and question answering.
• Scalability: Self-Attention scales better to large datasets and models, as it avoids the sequential bottleneck of RNNs.

For example, in translating "The cat, which is fluffy, sleeps" to French, Self-Attention ensures "fluffy" is correctly associated with "cat," producing an accurate translation like "Le chat, qui est fluffy, dort."

Differences from Standard Attention

While both Self-Attention and standard Attention (as used in Seq2Seq models) use queries, keys, and values to compute weighted sums, they differ in their application and scope:

• Scope of Attention:
  • Standard Attention: Used in Seq2Seq models, where the decoder attends to encoder hidden states. For example, in translation, the decoder focuses on the English input sequence (encoder states) to generate French words.
  • Self-Attention: Applied within a single sequence (input or output). Each word attends to all words in the same sequence, allowing the model to understand internal relationships (e.g., "cat" and "fluffy" in the input).
• Input to Attention:
  • Standard Attention: Queries come from the decoder’s hidden state, while keys and values come from the encoder’s hidden states.
  • Self-Attention: Queries, keys, and values all come from the same sequence (e.g., the input embeddings or hidden states of the same layer).
• Purpose:
  • Standard Attention: Aligns the output sequence with the input sequence, focusing on relevant input parts for each output word.
  • Self-Attention: Builds a contextual representation of the sequence itself, capturing relationships between its own words.

In mathematical terms, both use similar formulations (e.g., scaled dot-product attention), but Self-Attention applies it internally:

Position-Agnostic Issue and Positional Encoding

A key limitation of Self-Attention is that it is position-agnostic. It treats the input sequence as a set of words, not an ordered sequence, because it computes attention weights based solely on content (queries and keys), ignoring word positions. For example, "The cat chased the dog" and "The dog chased the cat" would have identical Self-Attention outputs, as the mechanism doesn’t know which word comes first.

In NLP, word order is critical (e.g., subject-verb-object changes meaning). To address this, Positional Encoding is added to the input embeddings to encode the position of each word in the sequence.

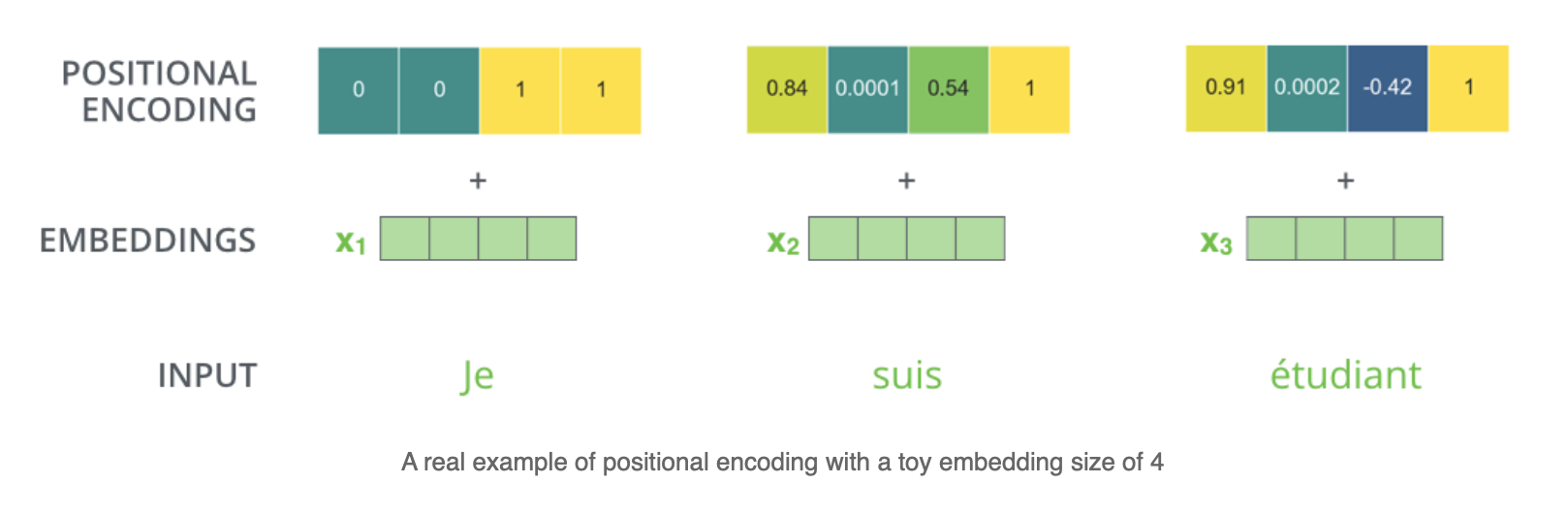
What is Positional Encoding?

Positional Encoding adds a vector to each word’s embedding that represents its position in the sequence. This vector ensures the model can distinguish "cat" in position 2 from "cat" in position 5. The Transformer model uses fixed sinusoidal functions for positional encodings, defined as:

Where:

• pos is the word’s position in the sequence (e.g., 1, 2, 3).
• i is the dimension index (0 to d_model/2).
• d_model is the embedding dimension (e.g., 512).

These sinusoidal functions create unique, periodic patterns for each position, allowing the model to learn relative positions (e.g., "word 3 is two positions after word 1"). The input to the model becomes:

Alternatively, positional encodings can be learned (trainable parameters), but fixed sinusoidal encodings are often used because they generalize well to longer sequences.

Why Positional Encoding Works

• Order Awareness: Adds position information to each word’s representation, enabling the model to distinguish word order.
• Relative Positioning: Sinusoidal patterns allow the model to learn relationships between positions (e.g., "two words apart").
• Scalability: Fixed encodings work for any sequence length, unlike learned encodings, which are fixed to a maximum length.

For example, in "The cat chased the dog," positional encodings ensure "cat" (position 2) and "dog" (position 5) have distinct representations, allowing Self-Attention to capture the correct subject-object relationship.

Linearity Problem and Feed-Forward Networks

Self-Attention is a linear operation because it computes a weighted sum of value vectors:

To address this, a Feed-Forward Neural Network (FFNN) or Multi-Layer Perceptron (MLP) is applied to each word’s attention output independently. In Transformers, the FFNN is applied after Self-Attention in each layer:

Where:

• x is the output of Self-Attention for a word.
• W₁, W₂ are weight matrices, and b₁, b₂ are biases.
• max(0, ·) is the ReLU activation, introducing non-linearity.

The FFNN transforms each word’s representation, allowing the model to learn complex patterns. For example, it can capture non-linear interactions like "not happy" implying negative sentiment, which a linear operation might miss.

Why FFNN Helps

• Non-Linearity: Introduces non-linear transformations, enabling the model to model complex relationships.
• Per-Word Processing: Applied independently to each word, maintaining parallelization benefits.
• Expressiveness: Increases the model’s capacity to learn intricate patterns in data.

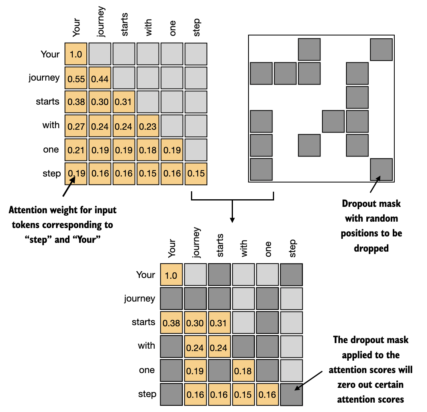
Masked Self-Attention for Generative Tasks

In generative tasks, like language modeling or machine translation, the model generates output words one at a time, using only the words it has already produced. For example, when generating "Je t'aime," the model predicts "t'aime" based on "Je," not future words like "aime." Masked Self-Attention ensures the model only attends to previous words in the sequence, preventing it from "cheating" by looking at future words.

How Masked Self-Attention Works

In standard Self-Attention, each word attends to all words in the sequence, including future ones. In Masked Self-Attention, a mask is applied to the attention scores to block attention to future positions:

Where:

• eᵢⱼ is the alignment score between query qᵢ and key kⱼ.
• j > i indicates future positions, set to negative infinity before softmax, resulting in zero attention weights.

The mask is typically a triangular matrix (1s on and below the diagonal, 0s above), ensuring word i only attends to words at positions 1 to i.

Why Masked Self-Attention?

• Causal Generation: Ensures the model generates words sequentially, using only past and current context, mimicking real-world generation.
• Training Efficiency: Allows parallel training of generative models by masking future tokens, unlike RNNs, which require sequential processing.
• Application in Decoding: Used in the decoder of Transformers for tasks like translation, where the output sequence is generated autoregressively.

For example, in generating "Je t'aime," Masked Self-Attention ensures "t'aime" is predicted based only on "Je," preventing the model from using "aime" prematurely.

Practical Example

Let’s build a Transformer-based model for translating English to French using a small parallel corpus. The encoder uses Self-Attention to process the English sentence (e.g., "I love you"), with positional encodings added to word embeddings to capture word order. Each word attends to all others, creating context-aware representations (e.g., linking "love" to "you"). The decoder uses Masked Self-Attention to generate the French translation ("Je t'aime") word by word, attending only to previous words in the output sequence (e.g., "t'aime" attends to "Je"). A Feed-Forward Network is applied after each attention layer to introduce non-linearity, enhancing expressiveness. This model leverages Self-Attention’s parallelization, positional encodings for order, and masking for autoregressive generation, outperforming RNN-based Seq2Seq models in accuracy and speed.